plus/minus epsilon

A One-Time Attribute-Based Signature scheme allows a signer, who posses a set of attributes verified by an authority, to sign a message with a predicate that is satisfied by his attributes. The signature can reveal no more about the signer than the predicate requires, and it should be infeasible to link multiple signatures to the same signer (signatures should be anonymous). Multiple users, each with only a strict subset of the required attributes to satisfy a predicate, should not be able to collude and forge a signature that does satisfy the predicate (the scheme should be collusion-resistant).

While there has been a fair amount of work on attribute-based signatures, all of the existing constructions are, quite frankly, nearly impossible to implement correctly or efficiently. They all rely on particularly abstruse and scarce primitives like bilinear pairings and monotone span programs, which only serve to restrict their usage in practice. [1]

Here, I propose a space and time efficient one-time attribute-based signature scheme based exclusively on one-way hash functions and asymmetric signature schemes--both of which are exceedingly efficient as well as widely understood and implemented in code, at the cost of a slightly looser anonymity guarantee. For the sake of usability, I focus on the use case where predicates are defined publicly before any message is signed--as it would be if ABS were being used to enforce a distributed access control mechanism.

Uses

Attribute-based signatures are the natural choice for simple authentication in systems where a user's capabilities depends on an arbitrarily complex access control system.

Compared to PKI-based systems, where all of a user's credentials may be accessible from their public key and signers are explicitly required to sacrifice anonymity, ABS schemes can offer absolute or revocable anonymity by only revealing the fewest number of attributes that satisfies the predicate.

Because of the properties of one-time ABS, it is obviously more efficient than standard ABS constructions and public key infrastructures, making it preferable for use in systems where a user's attributes may change frequently or the attribute-issuing authority is computationally capable of handling the additional load. However, comparing the space efficiency of OTABS to similar one-time signature constructions, it is either similar in efficiency or slightly less efficient due to some functions that have to grow linearly in the number of attributes.

Definitions

A one-time attribute-based signature scheme ABS is specified by two randomized algorithms and two deterministic algorithms, with at least two parties participating: a signature trustee (who signs messages), an attribute authority (who is responsible for assigning and verifying a trustee's attributes).

AGen: Generates an authority's keypair. Run by the authority exclusively. Takes as input a security parameter k exclusively. Outputs (APK, ASK), an Authority Public Key, and an Authority Secret Key.

TGen: Generates a trustee's keypair. Run by the authority exclusively, also. Takes as input a security parameter k and a set A of this trustee's attributes. Outputs TSK, a Trustee Secret Key.

Sign: Signs a message. Run by trustees exclusively. Takes as input a trustee private key TSK, a set A which is a subset of the trustee's attributes that he wishes to sign the message with, and the message m to be signed. Outputs s, a signature.

Verify: Verifies a signature on a message. Run by any party. Takes as input an authority public key APK, a candidate message m, and a candidate signature s. Outputs true or false.

Cryptographic Mechanisms

Merkle trees and Merkle-Winternitz chains are the primary mechanisms underlying this construction. In the event the reader isn't familiar with either, Merkle trees are well documented here and there's an in-depth discussion of Merkle-Winternitz chains in section 4.6 of reference [2].

Construction

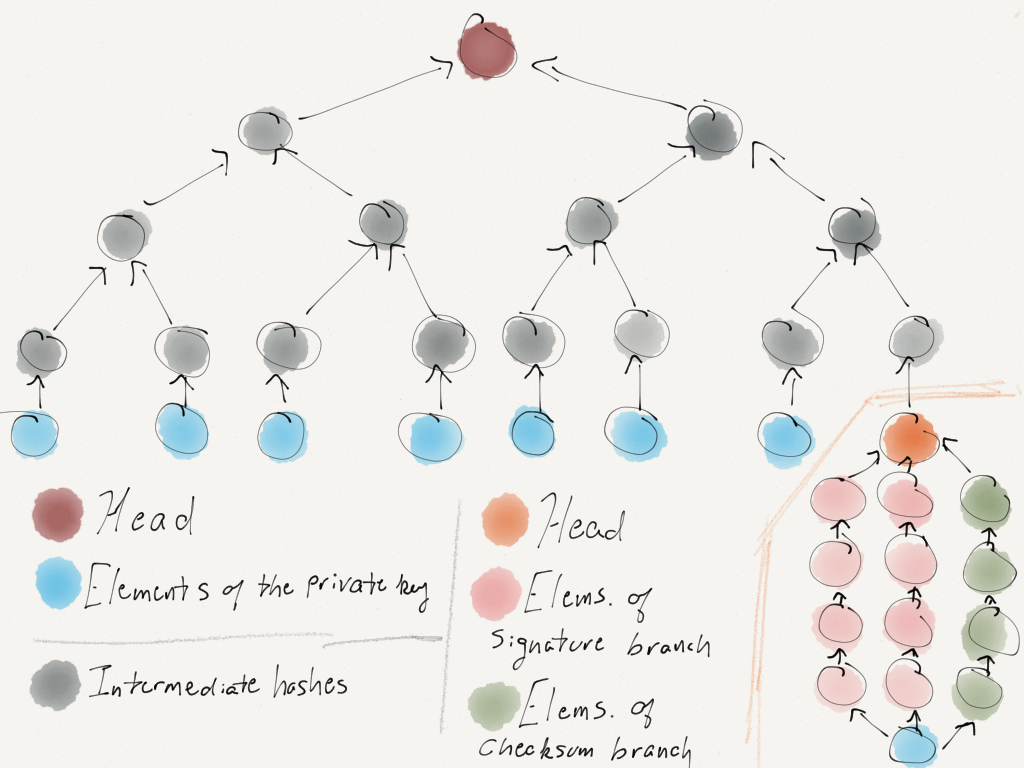
Above is the anatomy of a trustee's secret key in this construction. All of the blue elements (besides the one on the far right) represent the trustee's normalized attributes. The blue element on the far right represents a random string chosen by the attribute-issuing authority. The arrows, showing the application of a one-way function, describe the generation of a Merkle tree where the right-most leaf node is the head of a MW-chain. The head of the Merkle tree in its entirety is then the commitment from which the one-time signature and all the attributes the trustee wishes to prove are verified.

To authenticate the tree, the attribute-issuing authority simply signs the head of the tree and provides the signature as part of the secret key.

Once the authority has securely sent the secret key to the trustee, the trustee can generate a signature for any given message by using the MW-chain as normal and by publishing the authority's signature, the MW-chain signature, and a proof that the tree contains enough elements to satisfy some predicate.

It's out of the scope of this post to discuss the actual encoding/decoding/execution of some kind of predicate.

Lastly, per usual, in the below algorithms, issues of type are ignored.

Generating the Authority's Keypair

For the attribute-issuing authority to generate the master keypair, they choose a digital signature scheme such as DSA or ECDSA, and:

1. Calculate (MPK, MSK) = DSA.KeyGen(), a master public key and a master secret key.

The master public key is then securely published.

Generating the Trustee's Secret Key

For the attribute-issuing authority to generate a trustee secret key:

1. Normalize all of the trustee's attributes into a set of values A with cardinality 2^k - 1.
2. Choose a random string with the same length as the output of the one-way function, x.
3. Set x as the private key of a MW-chain and compute the corresponding public key, y.
4. Define A~ = {y} u A and compute the head of the Merkle tree over A~.
5. Compute sig = DSA.Sign(MPK, head)

The trustee is then securely sent the output (A, x, sig).

Signing a Message

A trustee computes a signature on a message m with predicate P by:

1. Determine the smallest preferable set of attributes A^ from A that satisfies P.
2. Calculate the set A~ by iterating through every element in A. If the current element is a member of the set A^, add the raw element to the set. Else, apply a one-way function to the element and add the output to the set.
3. Calculate the signature otsig by signing the message m with a MW-chain with private key x.

The trustee then publishes the output Sig = (sig, A~, otsig).

(What I've used here is a fairly naive scheme to compress the set A~, but another idea would be to disclose higher elements in the tree when possible, or to ask the authority to only commit to attributes that are pertinent.)

Verifying Signatures

An outside party verifies a signature Sig on a message m with predicate P by:

1. Calculate the set A^ from A~ by extracting the elements that aren't hashed/masked.
2. If the set A^ doesn't satisfy the predicate P, then return false.
3. Apply a hash to all of the unhashed elements of A~.
4. Use the message m to compute the MW-chain signature otsig's public key, y.
5. Define A~ = {y} u A~ and compute the head of the Merkle tree over A~ (sans the initial masking).
6. Calculate ok = DSA.Verify(MPK, head, sig) and return the output ok, true or false.

Hiding Attributes

As mentioned earlier, this construction has a looser anonymity guarantee than others, because some attributes have to be disclosed in full--which can certainly be useful in scenarios where the predicate explicitly requires identifying information. For example, if the predicate requires that the trustee have the attribute Name: Charlie Eppes, then there's no point in wasting time or space on a zero-knowledge proof of knowledge.

And while little to nothing can be done for tests for equality in general (besides finding a desirable way to divvy up a trustee's attributes), there's still hope for tests for inequality (>, <, or !=). The solution being, to treat each bit as an attribute rather than to conjoin them into one, so that the fewest number of bits can be revealed.

Instead of Level: 5, we would have: Level[2] = 1, Level[1] = 0, Level[0] = 1.

This would allow the trustee to prove that they possess a level greater than 0 by only disclosing Level[0], or to prove possession of a level greater than 1, 2, or 3 by disclosing Level[2] only.

This notion extends naturally into other operators.

Analysis

Assuming ECDSA-256, x as the number of bits that the hash function outputs and n as the number of attributes:

1. The trustee secret key is approximately xn + x + 64 = x(n + 1) + 64 bytes.
2. A signature is approximately 64 + xn + 22x = x(n + 22) + 64 bytes.

• SHA-1 with 10 attributes yields: 284, 704
• SHA-256 with 10 attributes yields: 416, 1088
• AES with 10 attributes yields: 240, 576

References

1. "Attribute-Based Signatures"
2. "Efficient Security Mechanisms for Routing Protocols"